Keep Innovating! Blog

1. はじめに
初めまして、技術創発推進室の新人AIエンジニアの松原と申します。私は学生時代からディープラーニングを使いはじめ、昨年にはE資格を取得しました。最近は、ディープラーニングを使った画像の異常検知技術の研究開発に取り組んでいます。その関連で調査した論文に面白いものがあったので、今回はそれを紹介してみようと思います。
タイトルは、"Modeling the Distribution of Normal Data in Pre-Trained Deep Features for Anomaly Detection” 、著者は, Oliver Rippel/Patrick Mertens/Dorit Merhofという方々です。原文はおなじみ arXiv にあります。
https://arxiv.org/abs/2005.14140
2. TL;DR
まずここで、全体の要約として本論文の結論を書きます。それは、
「"EfficientNet"(画像分類の分野で論文執筆当時のSoTA)の学習済みモデルを用いて正常画像の特徴量分布を求めることで、ゼロからモデルの構築・学習をすることなく異常検知モデルを作成でき、SoTAを達成できた!」 というものです。
この手法の基本的なアイディアは、性能の良い学習済み画像分類モデルがあるなら、そのモデルから得られる特徴量を取り出して流用すれば上手くいくのでは?という転移学習の発想にあるようです。
また、論文の後半ではこの手法がなぜ良い性能を出せるのか、筆者らはいくつかの仮説を立てて検証を試みています。
では、以下で論文の中身を順を追って説明します。
3. この論文の位置づけ・面白いポイント
3.1. 画像の異常検知の問題設定
まず、画像の異常検知の問題設定について確認しておきましょう。異常検知というタスクに特有な問題設定として、下記があります。
- そもそも異常はまれにしか起きない現象なので、採取できる異常データ数が少ない
- 異常を正確に定義するのが困難
すなわち、異常検知では学習に使えるのは正常画像がほとんどで、異常画像はまったく無いか、またはごく少量のみであり、さらに、異常の種類や性質などについて完全な定義がないことが前提条件となります。
3.2. 従来の手法
これまで提案された異常検知の手法には、以下の2つが多いと著者は述べています。
3.2.1. 正常データのみによる学習法
前述の問題設定により、画像の異常検知の手法でまず多いのが、正常データのみによる学習のアプローチをとるものです。例えば、オートエンコーダを用いた再構成型のモデルを使って正常データの特徴表現をゼロから学習し、それを異常検知に用いるという方法がいくつも提案されています。
3.2.2. 事前学習法
一方、使える教師データの数が偏っていたり少なかったりする状況での機械学習問題(半教師あり学習)と捉えると、ゼロから学習するのではなく、別のデータセットで事前学習を行うという方法が考えられます。しかし、その方向での研究例はまだ少ないようです。
3.3. この論文が提案している手法
この論文で提案される異常検知の手法は、前記3.3.2. の事前学習型です。用いる学習データは正常データのみです。事前学習モデルは、画像分類タスクで現在(論文執筆時点)の最高性能を持つとされる EfficientNet を用いています。
3.3.1. 学習フェーズ
学習の概略手順を述べると、
- (1)まず、 ImageNetに対して事前学習済みの EfficientNet に異常検知対象の正常画像セットを入力して推論させます。
- (2)次に、その際のモデル内部の特徴表現を取り出して、それを特徴ベクトルとして多変量ガウス分布で近似します。
- (3)最後に、こうして得られた分布を正常画像の分布とします。
となります。
3.3.2. 推論フェーズ
推論=異常検知フェーズでは、対象画像を EfficientNet に入力し、その内部特徴表現が上記で学習した正常画像の分布からどれくらい離れているのか、マハラノビス距離を使って判定します。一定以上離れていれば異常、そうでなければ正常という判断をします。
ある意味シンプルな手法と思えますが、MVTecの異常検知データセットにおいて過去最高の異常検知性能を達成したそうです。
3.4. この手法の分析
さらにこの論文では、著者らは事前学習した特徴表現の判別性能について分析しています。学習時に用いる正常データに対する特徴表現をPCA(主成分分析)で評価しているのですが、分散が小さい主成分であるほど、異常検知での判別性が高くなるという傾向が見られたそうです。またそうした判別性の良い成分は、事前学習を使わなければ(=ゼロからの学習では)獲得が困難であることも示唆されているようです。
この結果は、事前学習を使った異常検知を実施する場合に、どの特徴量を選択するかという判断に使えそうなので、とても面白い分析だと思います。
では、この手法について詳しく見ていきましょう。
4. 具体的な手法・理論
4.1. 多変量ガウス分布とマハラノビス距離
前章でも述べたとおり、提案手法では学習済みモデルによって抽出された特徴ベクトル  は以下の式で定義される多変量ガウス分布に従う、と仮定します。
は以下の式で定義される多変量ガウス分布に従う、と仮定します。
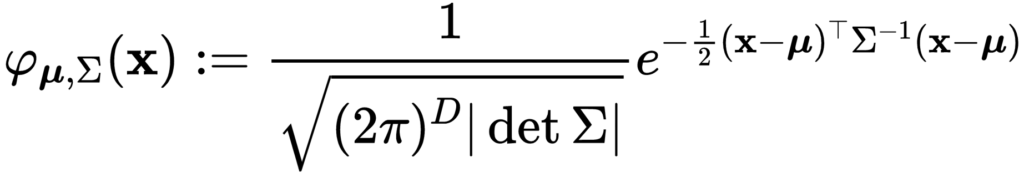
ここで、 は次元数、
は次元数、 は平均のベクトル、
は平均のベクトル、 は正定値共分散行列をそれぞれ表します。
は正定値共分散行列をそれぞれ表します。
さらに、本手法ではこの分布上の距離を測る手段としてマハラノビス距離を用います。
マハラノビス距離は多変量変数(=ベクトル型の変数)を扱う際に、要素(=ベクトルの成分)間の相関関係を考慮した上で変数同士の距離を計算することが可能なため、外れ値検出・異常検知の問題でよく使われます。
本手法でも、特徴ベクトル は多変量変数である、と仮定していますので、マハラノビス距離を採用しています。
は多変量変数である、と仮定していますので、マハラノビス距離を採用しています。
マハラノビス距離は以下の式で定義されます。
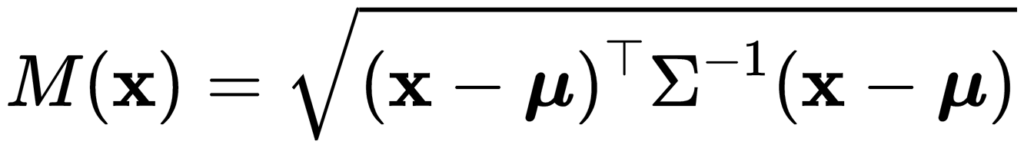
上記の式を見ると分かる通り、マハラノビス距離は多変量ガウス分布の平均ベクトルと共分散行列の逆行列から求めることができます。
また、マハラノビス距離の定義から  は自由度が
は自由度が の
の (カイ)二乗分布に従うことが知られており、その分布は以下の確率密度関数
(カイ)二乗分布に従うことが知られており、その分布は以下の確率密度関数 と累積分布関数
と累積分布関数 で定義されます。
で定義されます。
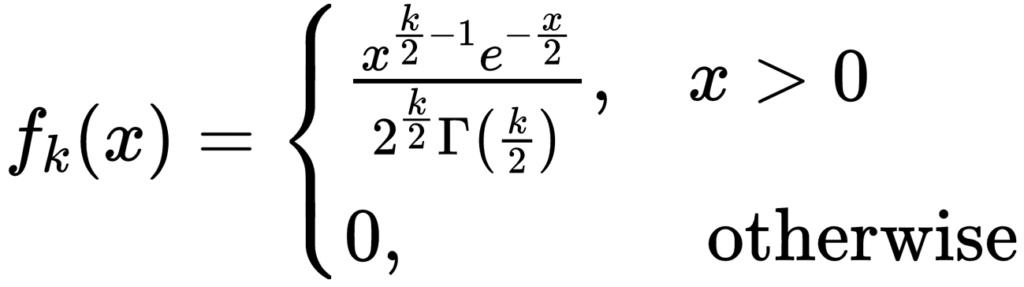
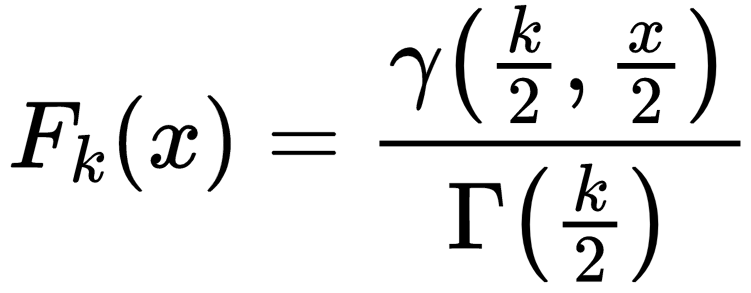
ここで、 は、
は、 でのガンマ関数です。また、
でのガンマ関数です。また、 は、第一種不完全ガンマ関数として知られている関数です。
は、第一種不完全ガンマ関数として知られている関数です。
4.2. 多変量ガウス分布のにおけるパラメータの推定法
前節で特徴ベクトルは多変量ガウス分布に従うと仮定しました。ここでは、その分布の具体的な形を求める方法を説明します。すなわち、分布のパラメータである平均と共分散行列をデータから求めるという問題です。これは確定的には解けない問題なので、特徴量データ を使って何らかの方法で推定する必要があります。
を使って何らかの方法で推定する必要があります。
そこで、学習フェーズで得られる特徴ベクトルは「多変量ガウス分布からサンプリングされた標本である」と考えて、統計学で使われる一般的な推定法を使います。
具体的には、平均を標本平均で推定し、共分散行列を以下の式で推定します。
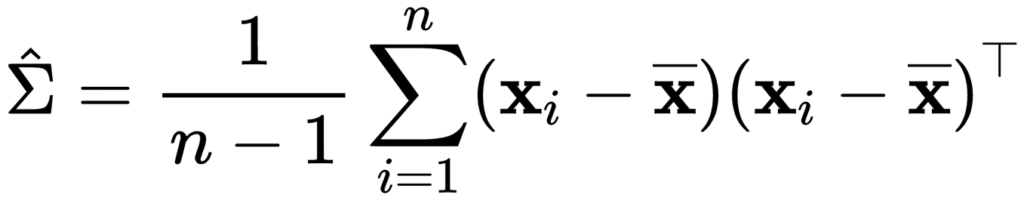
ここで、 は標本平均ベクトル,
は標本平均ベクトル, は標本のサイズです。
は標本のサイズです。
標本サイズ  が特徴ベクトルの要素数(次元数)より十分充分に大きい場合、上記の推定量を採用することで多変量ガウス分布を推定することができます。
が特徴ベクトルの要素数(次元数)より十分充分に大きい場合、上記の推定量を採用することで多変量ガウス分布を推定することができます。
一方で、標本サイズ  が十分に大きくない小さい場合には、共分散行列の定義から推定結果が不安定になる可能性があるという問題があります。さらに、標本サイズが小さくなり、特徴ベクトルの要素数を下回るより小さい場合は共分散行列が特異となってしまい、逆行列が求まらないという問題もあります。
が十分に大きくない小さい場合には、共分散行列の定義から推定結果が不安定になる可能性があるという問題があります。さらに、標本サイズが小さくなり、特徴ベクトルの要素数を下回るより小さい場合は共分散行列が特異となってしまい、逆行列が求まらないという問題もあります。
これらの問題を解決するために、本手法では共分散行列の推定について Ledoit, WolfらによるShrinkage法という手法を採用します。
Shrinkage法では、共分散行列の定義に基づいて計算された行列に一定の割合で単位行列を足し合わせることによって共分散行列の推定量を求めます。
具体的には以下の式で推定します。
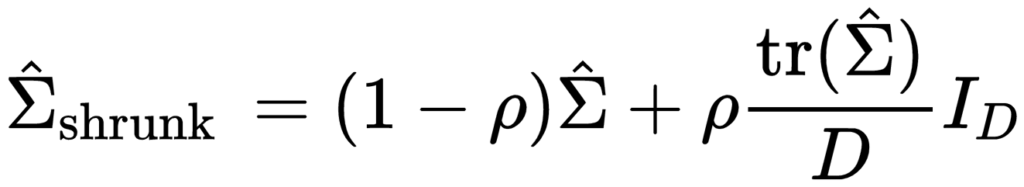
ここで、 は単位行列に対する重み付けを行うパラメータであり、バイアス・バリアンス間のトレードオフを調整するパラメータとして解釈することができます。
は単位行列に対する重み付けを行うパラメータであり、バイアス・バリアンス間のトレードオフを調整するパラメータとして解釈することができます。
ここまでで、特徴ベクトルが従う多変量ガウス分布の推定ができるようになりました。
4.3. 異常判定の方法としきい値の決定
前節までの議論で、分布の推定ができるようになったので、次は異常判定の方法について考えます。
既述の通り、異常判定の指標となる異常度は、推定した分布と対象画像の特徴ベクトルとのマハラノビス距離  を用いますので、これに対するしきい値を決める必要があります。
を用いますので、これに対するしきい値を決める必要があります。
多くの異常検知の手法では、検証データセットに対するROC曲線を使うなどして、所望のTNR(真陰性率)、もしくはTPR(真陽性率)となるように人間が経験的にしきい値を決めます。(ここでは Positive が異常、Negative が正常を意味します。)
一方、本手法ではマハラノビス距離が (カイ)二乗分布に従うことを利用し、次節で述べるように所望のFPR(偽陽性率)から異常度のしきい値を理論的に一意に算出できます。
(カイ)二乗分布に従うことを利用し、次節で述べるように所望のFPR(偽陽性率)から異常度のしきい値を理論的に一意に算出できます。
4.3.1. しきい値の算出方法
既述のとおり、マハラノビス距離は 二乗分布からサンプリングされたデータであると言えます。
二乗分布からサンプリングされたデータであると言えます。
このとき、正常データのマハラノビス距離の値が 二乗分布から得られる確率
二乗分布から得られる確率 を求めれば、この
を求めれば、この  はTNRと一致します。すると、
はTNRと一致します。すると、 の確率で異常データが得られることになるため、これをFPRの値とすることができます。
の確率で異常データが得られることになるため、これをFPRの値とすることができます。
この考え方により、本手法では許容できるFPRの値と 二乗分布の累積分布関数の2つを用いて計算した確率点
二乗分布の累積分布関数の2つを用いて計算した確率点  をしきい値とします。
をしきい値とします。
具体的には、 二乗分布の性質から、
二乗分布の性質から、 は以下の式を満たします。
は以下の式を満たします。
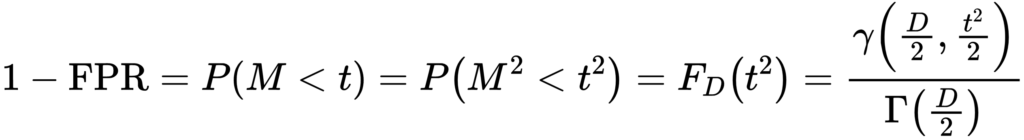
上記の式では累積分布関数は既知であるため、以下のように逆関数を計算することにより、 を求めることができます。
を求めることができます。
上記の式では累積分布関数 は既知であるため、以下のように逆関数を計算することにより、
は既知であるため、以下のように逆関数を計算することにより、 を求めることができます。
を求めることができます。
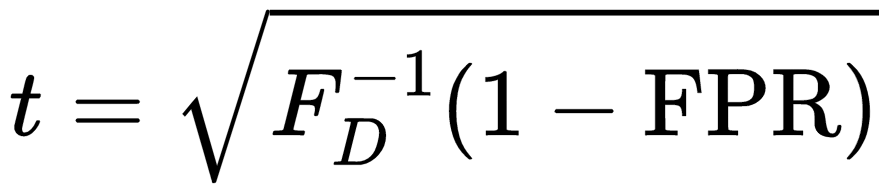
こうして求めたしきい値  と、異常判定の対象画像の特徴ベクトルとのマハラノビス距離の値を比較することで異常判定を行うことができます。
と、異常判定の対象画像の特徴ベクトルとのマハラノビス距離の値を比較することで異常判定を行うことができます。
5. 実験結果・考察
本論文ではMVTecの異常検知データセット(https://www.mvtec.com/company/research/datasets/mvtec-ad/)を用いて実験を行い、様々な観点から考察しています。
5.1. EfficientNetの構造と特徴ベクトル
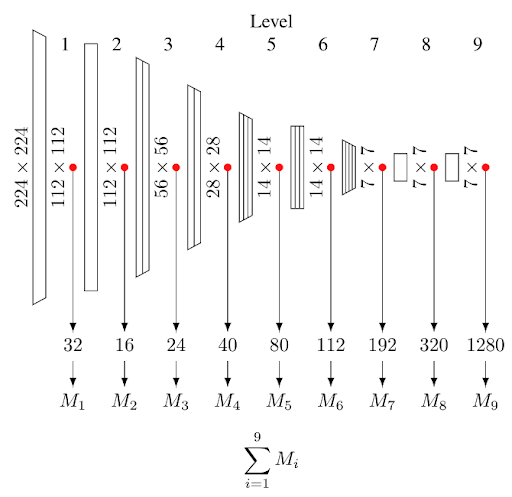
はじめに、EfficientNetの構造を簡単に説明します。EfficientNetとはAutoMLを使って作られた画像識別モデルをベースとして、それを7段階でスケールさせたモデルの総称です。ベースモデルはいくつかの層をまとめて1 levelとし、9個のlevelで構成され、スケールさせるモデルでは level 別に一定の割合で層の深さ、入力画像の解像度、レイヤーのサイズを増加させていきます。
本手法の異常検知では、まず対象画像を入力して得られる各levelの最終層の特徴量を取り出し、チャネルごとに平均を取ってベクトルに変換します。このベクトルについて、学習時に求めた多変量ガウス分布とのマハラノビス距離を計算します。マハラノビス距離は level 別の値9個と、全 level に対する各マハラノビス距離の合計値1個とを合わせて計10個を評価しています(図1)。
5.2. 提案手法の有効性の評価
5.2.1. 分布の仮定と異常度に関する評価
本手法で用いている、多変量ガウス分府やマハラノビス距離による異常検知の妥当性を評価するために、著者らは分布と異常度設定を以下のように設定した場合との比較を行っています。
- 分布: 分散固定の単変量ガウス分布, 異常度: 分布の平均値からの
 距離
距離 - 分布: 分散を固定しない単変量ガウス分布, 異常度: 分布の平均値からの標準化ユークリッド距離(SED)
EfficientNetのステージ別にこの設定でそれぞれ評価を行い、表1の結果が得られました。
表1 特徴層別の AUROC およびSEM(平均からの標準誤差)のパーセント値。EffcientNet-B4について、それぞれ異なる異常度(L2, SED, Mahalanobis)を適用したもの。
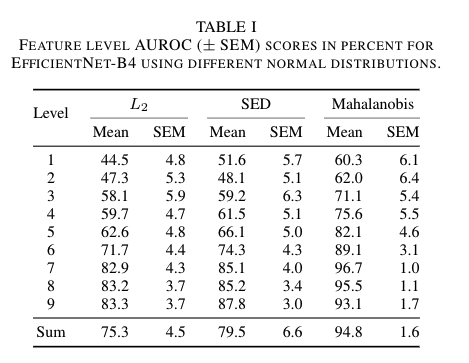
表1の "Mahalanobis"の列が本手法の結果です。これにより、本手法が精度とロバスト性において最もよい結果を示したことが分かります。
さらにその Level 別の結果を見ると、Level1 から順に Level が深くなるにつれて精度が向上していきますが、ある一定の Level を超えると精度が下がっていくことが分かります。これは EfficientNet が画像の一般的な特徴量を獲得できているのは、ある一定の Level の層まで(この例では Level7 まで)であり、それより大きい Level の層は ImageNet 特有の特徴量に適合した値になっているからではないかと著者らは推測しています。
5.2.2. モデルのアーキテクチャに関する評価
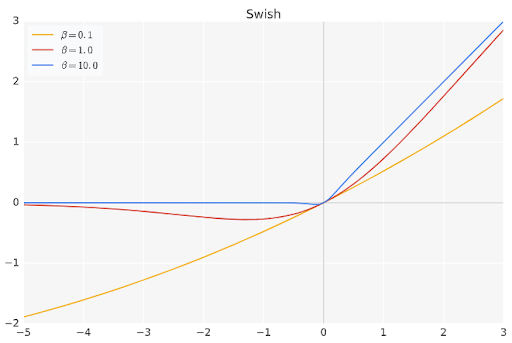
EfficientNet を採用することの有効性を評価するために、著者らは ResNetとの精度比較を行っています。結果は全体として EfficientNet の方が良い精度になっています。これは 一つには、画像分類において高性能を達成している EfficientNet の効率的な構造が貢献していることと、もう一つは、そこに使用されている活性化関数 Swish の出力特性が関係しているのではないかと筆者らは考察しています。
ResNetで使用されている活性化関数は ReLU です。ご存知のように、ReLUでは、入力値がマイナスの場合は出力はすべて0になります。上記の ResNet との精度比較において、ReLU を適用した後に得られる特徴量から算出した異常度計算では、ReLUがいくつかの特徴量を 0 に丸めてしまうために、実際にしばしば異常判定に失敗している、としています。
それに比べて Swish では、入力値がマイナスの領域においても、ゼロではない出力値を持っていますので、ReLUのように特徴量の情報が完全に消えてしまうことはありません(補足図1)。これが精度向上につながっていると考えられます。
5.2.3. EfficientNetのスケールの違いの評価
既に述べたように、EfficientNetにはモデルの大きさをスケールさせたバージョンがあり、B0~B7まで存在します。
より大きなモデルを使う方が ImageNet の識別に対してはより良い精度を示すのですが、本手法の異常検知ではそうはならないそうです。
実験で検証してみると、一定のスケールを境に異常検知の精度が飽和し始め、それ以上大きなモデルとなると少し精度が下がります。これは、モデルのスケールが大きくなるほど ImageNet に対して過学習を起こしていて、汎用的な特徴量を学習していない可能性を示しています。
5.3. なぜ事前学習済みモデルが有効なのか
次に著者らは、本手法の転移学習アプローチや多変量ガウス分布がなぜ性能が良いのか調査を試みています。それは、「異常検知に必要な特徴量は正常データ内では必ずしも強く変化していない」という仮説を立てて、それを検証していくという形になっています。
特徴量の変化の影響を調べるため、多変量ガウス分布に当てはめる前の特徴量に対して主成分分析(PCA)を行います。そして、分散の小さな成分、または大きい成分を次元削減して精度評価を行いました。
分散の小さな成分の削減をした場合、1%を削減(これをPCA99%と呼びます)するだけで異常検知精度の低下が見られました。一方で、分散の大きな成分を削減する場合では上位 99.99%の成分を削減(これを NPCA 0.01% と呼びます)しても、次元削減を行わない時と近い水準の精度を維持できました。
この結果は正常データ内における、分散の小さい主成分が異常検知に対して支配的に働いていることを示しています。
以上のような理由により、著者らは、「正常データのみを使ってゼロから学習を行う異常検知手法のほうが、事前学習済みモデルから得られた特徴量を使う異常検知手法(=本手法)よりも精度が劣ることを示唆している」としています。でも、この結論はちょっと分かりにくいと思いませんか? この部分は原論文でも短くあっさり書かれているだけなので、以下は私の解釈になりますが、たぶんこういうことです。
正常データのみのゼロからの学習では、当然ながらモデルは正常データ群の特徴量の範囲だけを表現しようとして学習を行います。いわば、正常データ群の特徴空間だけを虫眼鏡で拡大して見ているようなイメージであり、正常データ群内で分散の大きな特徴ほど優先的に重み付けられる形で学習するでしょう。そのため、上記のPCA実験結果が示している、異常検知で重要となる「分散が小さい特徴」を上手く学習できるとは限らないことになります。
5.4. 異常度のしきい値設定
4.3.節で説明したとおり、本手法では異常度のしきい値が所望のFPRより逆算できるとしています。しかし、このしきい値を用いて実際に異常判定を行うと、結果のFPRは所望のFPRとは異なっています。なぜなら、異常判定の基礎となる正常データの多変量ガウス分府は、あくまでも推定値であり、誤差を含んでいるからです。
これを確かめるために、分布の推定(=共分散行列の推定)の精度変化がしきい値の推定にどのように影響するかを調べるため、筆者らは学習データのオーグメンテーションを行って評価しています。これは学習データが多いほど、共分散行列の推定精度が向上するためです。さらに主成分分析による次元削減の条件も組み合わせてそれぞれ精度を評価しています。(表4)
表4 期待FPRと実際のFPR
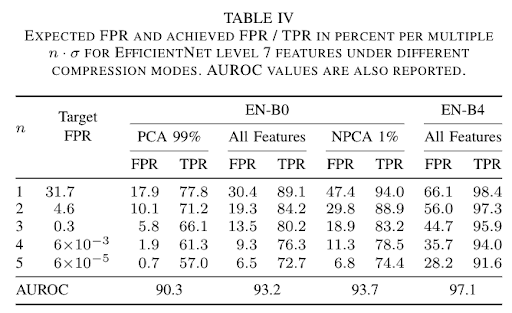
結果として、学習済みモデルから得られた特徴量から分散の小さな主成分を削減し、かつ EfficientNet-B0 のようなスケールの小さいモデルの時のみ、所望のFPRの設定に近い結果が得られました(表1のEN-B0 の PCA99%の列)。言い換えると、本論文の理論は大きく間違ってはいないが、モデルのスケールに対してデータが少ない場合は、所望の FPR に基づくしきい値計算は難しいということになります。
これは、より複雑なモデルでは、訓練データから得られる特徴表現が訓練データに存在するノイズに対して過学習している可能性を示唆しており、それを確かめるには、より大きい訓練データセットによって再評価すべきだろうと筆者らは述べています。
6. まとめ
この論文では、EfficientNet という現在SOTAの性能をもつ画像分類モデルを利用して、画像から質のよい特徴量を抽出し、それを多変量ガウス分布に当てはめることでマハラノビス距離による異常度を計算できるようにし、MVTecデータセットの全15種類について、AUROC 95.8%前後という、精度の良い異常検知を実現しています。
ゼロから学習することなく、汎用的で性能の良い異常検知を実現できる可能性を示した点は素晴らしいと思います。
また、PCAを使った特徴量の分析により、異常検知において重要な特徴量の主成分とはどのような性質を持っているのかについて、いくつかの興味深い知見を明らかにしました。これらは、今後の研究のヒントとなりそうです。
7. おわりに
AIのモデルをゼロから開発するのはかなり大変なことです。モデルを全て自前で設計・コーディングし、目標とする精度を出すには多くの時間を要することもありますし、またそれが精度を確約できるということもありません。
一方、この論文が提案しているように、既存のモデルを利用して開発するという方法があります。オープンで実績のあるモデルからの転移学習やファインチューニング、ドメイン適応、さらに今回の論文の手法のようにモデルの中間出力を利用するなど、既存モデルを活用するための様々なアプローチの研究が最近盛んに行われています。
これが意味していることは、AIに関する情報を集め、それらを組み合わせることで、強力で驚くべき技術を実現できる可能性が出てくるということです。これは簡単な仕事ではないと思いますが、従来の個別にモデルを開発していた段階よりも大きな前進ではないかと思います。
このように世界中の研究者が作り上げた高度なAIを組み合わせて、新たな機能や価値を作り出せることは、AI技術の魅力の一つであると思います。
特にAIのPoCや実務活用などの場面で、素早く結果を得るためには、既存のAIを賢く利用していくことがこれから必要になっていくのではないでしょうか。私も、今後そうしたスキルや知見を高めていきたいと考えています。
今回の記事は以上です。最後まで読んでいただき、ありがとうございました!
- テレワーク
- リリースノート
- リネージ管理
- knitfab
- OpeN.lab
- ChatGPT
- 画像生成
- 画像認識
- 書籍紹介
- 対話
- 自然言語処理
- Open Innovation
- アカデミック
- 活動報告
- ビジネス
- ガジェット
- オープンイノベーション
- TIPS
- 線型代数
- 数学
- Airflow
- 論文紹介
- MediaPipe
- 顔認識
- 可視化
- 異常検知
- プラモデル
- イノベーション
- 自動運転
- AI
- MLOps
